周末两次的鸿运宝箱,肯定让很多玩家着迷不已,那么它的运行机制到底是什么样子?到底是发宝箱的玩家收益多还是开宝箱的玩家收益多,肯定很多玩家心存疑惑,攻略组bobo运用仿真建模的方法带你揭示鸿运宝箱的运行机制?
首先玩法抽象:
计算
庄家可以发放一定金额的奖池,规则:100万起步,必须是10万的整数倍,假设为x;玩家规则:开启奖池,需要投放一定金额,玩家自己不能控制,而是系统随机生成的一个10万至50万之间的一个数yi,中奖概率为生成的yi除以总奖池总额,若不能中奖,则将投入的yi计入总奖池;
游戏终止规则:
1、玩家中奖,可拿走x的0.95倍+所有玩家开奖投入(y1+y2+y3+..+yi),即系统收取0.05x的税;
2、庄家赢,当奖池累计到初步投入的2倍少10万时,庄家可拿走x的0.95倍+所有玩家开奖投入(y1+y2+y3+..+yi),即系统收取0.05x的税。举个例子,比如庄家投入100万,奖池累计至189万时,尚可以支持下一个玩家,游戏不会终止,允许下一个玩家继续玩一次;奖池累计至191万时,则直接返回给庄家,游戏终止。
中奖几率描述:给玩家生成的随机数为yi,则他的中奖概率为yi/(x+y1+y1+y2+....+y(i-1))
核心算法思想:
1、庄家赢的算法机制:yi由随机数random出一个10万-50万的数,sum构成一个x+y1+y1+y2+....+y(i-1)不断叠加的求和,至sum>2x-100000时中止。
2、玩家赢的算法机制:内层循环中,每次生成一个随机z,z的范围为0-1之间,如判定z
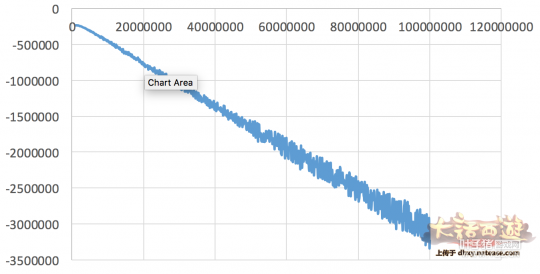
在庄家每个投入的n次计算上,取得均值,可得到下述收益的平滑曲线:
通过该收益曲线,可以看出,玩家和庄家的获胜概率基本相同,发放1亿时,庄家大约亏300万,并且可以得到进一步的重要结论:关于税收的5%,通过收益曲线的斜率,可近似得到庄家负担60%,玩家负担40%。
数理验证:庄家获胜概率p
为了更简化地得到答案,我们将玩家的投入均匀等分:
因此,在n较大时,我们通过数理计算的方式也可以近似地得到庄家获胜几率为1/2的结果,因此仿真结果具有较好的信度。无论是模拟仿真还是数理计算,均可知道,宝箱金额翻倍时中止的游戏设定,对玩家和庄家都比较公平。
因此,我们可以得到如下结论:
1、鸿运宝箱是一个设计的比较公平的游戏,发宝箱的和开宝箱的期望收益基本上都是55开,双方的胜负机会均等,也就意味着,只要进行足够多次,收益也就都会基本会稳定,且为负,不存在哪一方在先天的游戏机制上占便宜的情况。
2、鸿运宝箱因为系统需要扣除初始金额的5%,因此是一个负和博弈的过程,在这个过程中损耗的支出,通过模拟仿真可以得到,发宝箱的玩家负担其中的60%,开宝箱的玩家负担40%,也就意味着,如果游戏进行无穷多次,发宝箱玩家损失发箱金额总额的3%,开宝箱的玩家损失累计开宝箱总金额的2%。
看到了这样的计算和仿真结果你还开不开箱子呢?
PS:可能存在误差的原因,游戏里的随机数生成机制和该次实验编程采取的生成机制不同,毕竟都是伪随机数。
<<<点击进入大话西游手游论坛讨论>>